Bagaimana cara membaca Fibonacci

Fibonacci adalah deret angka yang menarik. Setiap angka dalam deret ini adalah jumlah dari dua angka sebelumnya. Misalnya, deret dimulai dengan 0 dan 1. Kemudian, angka berikutnya adalah 1, diikuti oleh 2, 3, 5, dan seterusnya. Banyak orang penasaran dengan pola ini.

Deret Fibonacci tidak hanya sekadar angka. Ia memiliki banyak aplikasi dalam berbagai bidang. Dari matematika hingga seni, bahkan dalam alam. Misalnya, banyak bunga dan daun mengikuti pola ini. Ini membuat Fibonacci menjadi topik yang sangat menarik untuk dipelajari.

Namun, bagaimana cara membaca dan memahami deret ini? Pertama, kita perlu mengenali pola yang ada. Setelah itu, kita bisa mulai menghitung angka-angka selanjutnya. Dengan latihan yang cukup, siapa pun bisa menguasai cara membaca Fibonacci dengan mudah. Mari kita jelajahi lebih dalam tentang keindahan dan kompleksitas deret ini.

Pengenalan tentang Deret Fibonacci

Sejarah dan Asal Usul Fibonacci

Deret Fibonacci adalah salah satu konsep matematika yang paling menarik. Ditemukan oleh seorang matematikawan Italia bernama Leonardo dari Pisa, yang lebih dikenal sebagai Fibonacci. Ia lahir sekitar tahun 1170 dan meninggal pada tahun 1250. Fibonacci memperkenalkan deret ini dalam bukunya yang berjudul "Liber Abaci". Buku ini diterbitkan pada tahun 1202 dan menjadi salah satu karya penting dalam sejarah matematika.

Deret Fibonacci dimulai dengan dua angka, yaitu 0 dan 1. Setiap angka berikutnya adalah hasil penjumlahan dari dua angka sebelumnya. Misalnya, urutan deretnya adalah 0, 1, 1, 2, 3, 5, 8, 13, dan seterusnya. Konsep ini sederhana, tetapi memiliki banyak aplikasi yang menarik dalam berbagai bidang.

Penerapan Deret Fibonacci dalam Kehidupan Sehari-hari

Deret Fibonacci tidak hanya penting dalam matematika, tetapi juga memiliki banyak penerapan praktis. Misalnya, dalam bidang keuangan, trader sering menggunakan deret ini untuk menganalisis pergerakan pasar. Selain itu, dalam ilmu komputer, algoritma Fibonacci sering digunakan untuk menyelesaikan masalah tertentu.

• Dalam seni, proporsi Fibonacci sering digunakan untuk menciptakan komposisi yang harmonis.
• Dalam biologi, banyak pola pertumbuhan tanaman mengikuti urutan Fibonacci.
• Dalam arsitektur, desain bangunan sering terinspirasi oleh rasio Fibonacci.

Dengan demikian, meskipun deret ini tampaknya sederhana, dampaknya sangat luas. Sejarah Fibonacci menunjukkan bagaimana satu ide dapat mengubah cara kita memahami dunia. Dari matematika hingga seni, deret Fibonacci terus mempengaruhi berbagai aspek kehidupan kita.

Metode Menghitung Deret Fibonacci

Deret Fibonacci adalah urutan angka yang dimulai dari 0 dan 1. Setiap angka berikutnya adalah hasil penjumlahan dari dua angka sebelumnya. Ini membuat deret ini sangat menarik dan mudah dipahami. Misalnya, urutan pertama adalah 0, 1, 1, 2, 3, 5, 8, dan seterusnya. Metode ini dapat dihitung dengan berbagai cara.

Metode Rekursif

Salah satu metode yang paling umum digunakan adalah metode rekursif. Dalam metode ini, fungsi memanggil dirinya sendiri untuk menghitung angka Fibonacci. Namun, metode ini bisa sangat tidak efisien untuk angka yang besar. Mengapa? Karena banyak perhitungan yang dilakukan berulang kali. Misalnya, untuk menghitung Fibonacci ke-5, fungsi akan menghitung Fibonacci ke-4 dan ke-3, dan seterusnya.

Metode Iteratif

Metode iteratif adalah alternatif yang lebih efisien. Dalam metode ini, kita menggunakan loop untuk menghitung angka Fibonacci. Dengan cara ini, kita hanya menyimpan dua angka terakhir, sehingga menghemat memori. Mari kita lihat contoh sederhana untuk menghitung angka Fibonacci ke-n menggunakan metode ini:

n	Fibonacci(n)
0	0
1	1
2	1
3	2
4	3
5	5
6	8

Selain metode rekursif dan iteratif, ada juga metode lainnya seperti metode matriks. Metode ini menggunakan sifat matriks untuk menghitung angka Fibonacci dengan cepat. Dengan menggunakan metode ini, kita dapat menghitung angka Fibonacci ke-n dalam waktu logaritmik. Ini sangat efisien untuk angka yang sangat besar.

Secara keseluruhan, ada banyak cara untuk menghitung deret Fibonacci. Setiap metode memiliki kelebihan dan kekurangan masing-masing. Pilihan metode tergantung pada kebutuhan dan konteks penggunaan. Namun, semua metode ini mengarah pada satu tujuan yang sama: untuk memahami dan menghitung angka Fibonacci dengan cara yang efektif.

Metode Menghitung Deret Fibonacci

Deret Fibonacci adalah urutan angka yang sangat menarik. Angka pertama adalah 0, diikuti oleh 1. Setiap angka berikutnya adalah jumlah dari dua angka sebelumnya. Ini menciptakan pola yang unik dan berulang. Metode untuk menghitung deret ini bervariasi, mulai dari yang sederhana hingga yang kompleks.

Metode Rekursif

Salah satu metode yang paling umum digunakan adalah metode rekursif. Dalam metode ini, fungsi memanggil dirinya sendiri untuk menghitung angka Fibonacci. Misalnya, untuk menghitung Fibonacci(n), kita perlu menghitung Fibonacci(n-1) dan Fibonacci(n-2). Meskipun mudah dipahami, metode ini tidak efisien untuk angka besar. Waktu komputasinya meningkat secara eksponensial.

Metode Iteratif

Metode iteratif adalah alternatif yang lebih efisien. Dalam metode ini, kita menggunakan loop untuk menghitung angka Fibonacci. Dengan menyimpan hasil sebelumnya, kita dapat menghindari perhitungan berulang. Ini mengurangi waktu komputasi secara signifikan. Metode ini sangat efektif untuk menghitung angka Fibonacci dalam jumlah besar.

Selain itu, ada juga metode menggunakan rumus Binet. Rumus ini memungkinkan kita menghitung angka Fibonacci tanpa iterasi atau rekursi. Meskipun rumus ini terlihat rumit, hasilnya sangat cepat dan efisien. Namun, akurasi dapat menurun untuk angka yang sangat besar. Ini karena keterbatasan presisi dalam perhitungan desimal.

Dengan berbagai metode ini, kita dapat memilih yang paling sesuai dengan kebutuhan. Setiap metode memiliki kelebihan dan kekurangan masing-masing. Penting untuk memahami konteks penggunaan setiap metode. Dengan demikian, kita dapat memanfaatkan deret Fibonacci secara optimal dalam berbagai aplikasi.

Aplikasi Praktis Deret Fibonacci

Deret Fibonacci memiliki banyak aplikasi praktis dalam berbagai bidang. Salah satu contohnya adalah dalam ilmu komputer. Algoritma yang menggunakan deret Fibonacci sering kali lebih efisien. Ini membantu dalam pengolahan data dan pencarian. Misalnya, algoritma pencarian Fibonacci dapat mempercepat proses pencarian dalam struktur data tertentu.

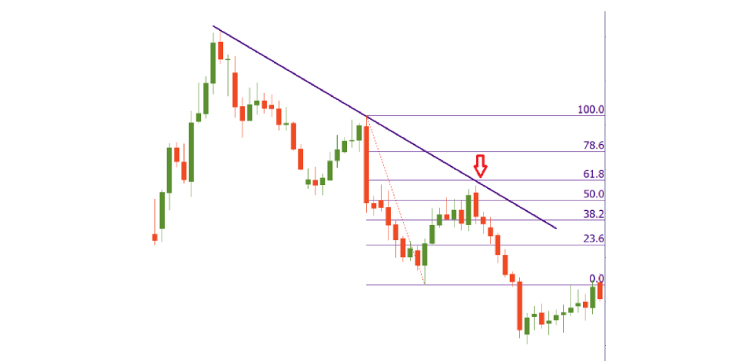
Selain itu, deret ini juga muncul dalam analisis pasar saham. Trader sering menggunakan rasio Fibonacci untuk menentukan level support dan resistance. Dengan menggunakan angka Fibonacci, mereka dapat membuat keputusan yang lebih baik. Ini adalah contoh bagaimana matematika dapat diterapkan dalam dunia nyata.

Di bidang seni, deret Fibonacci juga memiliki peranan penting. Banyak seniman dan arsitek menggunakan proporsi Fibonacci dalam karya mereka. Ini menciptakan keseimbangan dan keindahan visual. Misalnya, lukisan terkenal seperti "The Last Supper" oleh Leonardo da Vinci menunjukkan penggunaan rasio ini.

Dalam biologi, deret Fibonacci terlihat pada berbagai fenomena alam. Contohnya, jumlah kelopak bunga pada beberapa jenis bunga mengikuti pola ini. Selain itu, susunan daun pada batang tanaman juga sering mengikuti deret Fibonacci. Fenomena ini menunjukkan keterkaitan antara matematika dan alam.

Penggunaan deret Fibonacci dalam desain grafis juga semakin populer. Banyak desainer menggunakan proporsi ini untuk menciptakan komposisi yang harmonis. Dengan memanfaatkan rasio ini, mereka dapat menarik perhatian penonton. Hal ini membuat karya mereka lebih menarik dan estetis.

Secara keseluruhan, aplikasi praktis deret Fibonacci sangat beragam. Dari ilmu komputer hingga seni, deret ini memberikan kontribusi yang signifikan. Penggunaan angka Fibonacci membantu kita memahami pola dan struktur di sekitar kita. Dengan demikian, penting untuk mengeksplorasi lebih lanjut tentang deret ini dan aplikasinya dalam kehidupan sehari-hari.

Hubungan Fibonacci dengan Alam dan Seni

Deret Fibonacci dapat ditemukan di berbagai aspek alam. Misalnya, pola pertumbuhan daun pada tanaman sering mengikuti urutan ini. Dalam banyak kasus, bunga memiliki jumlah kelopak yang merupakan angka Fibonacci. Ini menciptakan keseimbangan dan keindahan yang alami.

Selain itu, banyak hewan juga menunjukkan pola Fibonacci. Contohnya, cangkang siput dan spiral galaksi mengikuti prinsip yang sama. Fenomena ini menunjukkan keterkaitan mendalam antara matematika dan biologi. Dalam banyak hal, deret Fibonacci membantu menjelaskan struktur yang kompleks dalam alam.

Di dunia seni, Fibonacci juga memiliki pengaruh yang signifikan. Banyak seniman dan arsitek menggunakan rasio emas, yang berkaitan erat dengan deret Fibonacci. Ini menciptakan komposisi yang harmonis dan menarik secara visual. Karya-karya terkenal, seperti lukisan Leonardo da Vinci, sering kali mencerminkan prinsip ini.

Rasio emas menciptakan ketertarikan visual yang mendalam. Misalnya, ketika kita melihat lukisan, mata kita cenderung tertarik pada titik-titik tertentu yang mengikuti pola Fibonacci. Hal ini menciptakan pengalaman estetika yang lebih memuaskan. Keseimbangan dan simetri yang dihasilkan membuat karya seni lebih menarik.

Dalam arsitektur, banyak bangunan terkenal juga mengadopsi prinsip Fibonacci. Struktur-struktur ini sering kali memiliki proporsi yang menyenangkan untuk dilihat. Dari Piramida Mesir hingga Katedral Eropa, semua menunjukkan hubungan ini. Ini menunjukkan bahwa matematika dan seni saling melengkapi dengan cara yang luar biasa.

Secara keseluruhan, hubungan antara Fibonacci, alam, dan seni sangatlah kuat. Deret ini tidak hanya sekadar angka, tetapi juga menciptakan keindahan. Dalam setiap aspek kehidupan, kita dapat menemukan jejak Fibonacci. Ini adalah pengingat bahwa matematika dan seni adalah dua sisi dari koin yang sama.